勉強。こちらが参考になった。
https://rindalog.blogspot.com/2017/07/regularizationridgelasso-elastic-net.html
https://jp.mathworks.com/help/stats/lasso-and-elastic-net.html
http://tekenuko.hatenablog.com/entry/2017/11/18/214317
https://aizine.ai/ridge-lasso-elasticnet/#:~:text=Elastic%20Net,%E3%81%A8%E3%81%97%E3%81%A6%E4%BD%9C%E3%82%89%E3%82%8C%E3%81%BE%E3%81%97%E3%81%9F%E3%80%82
- そもそも正則化って [Link]
- 機械学習に置ける正則化とは,過学習(Over-fitting)の回避が目的となっている.
- 下の例でいう、Θがどれかの値に偏るのを防ぐ
- Ridge回帰(L2正則化)
- Lasso回帰
- Θの絶対値をcost functionに入れたもの
- Lasso は、他の係数をゼロにして、幾つかの特徴変数を選ぶ。この特性は feature selection として知られ、Ridge にはないもの。
- L1 regularization(L1 正則化)を使ったもので、大量の変数からの選択で一般に利用される。
- Sparse modelingと関係性が深い(特徴量選択)。
- 論点
- Ridge を使った場合、係数は小さくなるが全ての変数は残る。問題は、依然として 10,000 個の変数があることで、これは悪い性能のモデルの原因になる
- この問題に Ridge ではなく、Lasso を使ったらどうなるか。相関する変数があると、Lasso Regression は相関関係にある変数のうちの一つを残し、他の変数をゼロとする。この場合の問題は、情報の喪失に有り、モデルの正確性を下げる
- ==>elastic net regression で知られる他の回帰分析がある。これは基本的には Ridge と Losso の混合。
- elastic net regression
- wikipediaより
- 相関関係にある独立変数がデータセットにあるとする。Elastic Net は相関関係にある変数のグループを作る。グループの変数の一つが強い予測子(依存変数と強い相関関係にある)の場合、グループの変数をモデルに含める。(Lasso のように)他の変数を除くのは、データの理解に必要な情報の欠落で、モデル性能を落とすことに繋がりかねない。
- 変数が多すぎてもダメ、変数を削りすぎてもダメ(情報消失)というジレンマは常に考慮すべきこと。
- この時の係数は、ridgeと同じく0は許さない???
- https://jp.mathworks.com/help/stats/lasso-and-elastic-net.html
- α = 1 の場合、Elastic Net は LASSO と同じになります ==> 許すのだろう。
- かんたんな解説
- リッジ回帰:「正則化された線形回帰の一つで、線形回帰に「学習した重みの二乗の合計(L2正則化項)」を加えたもの」です。L2正則化項による正則化では重みは完全に0にはならない性質があるため、説明変数が非常に多い時にはモデルの解釈が複雑になるという欠点があります。
- Lasso回帰:「正則化された線形回帰の一つで、線形回帰に「学習した重みの合計(L1正則化項)を加えたもの」です。不要と判断される説明変数の係数(重み)が0になる性質があり、モデルの選択と同時に説明変数の数を削減して、説明変数(特徴量)の選択を自動で行ってくれます。
- Elastic Net:リッジ回帰とLasso回帰の折衷案で「Lasso回帰のモデルに取り込める説明変数の数に制限がある」という問題点をカバーできる方法として作られました。
- 論点
- 今回のエミュレーターは優決定問題。なので、sparse modelingに代表される特徴量選択をしたかった。
- しかし、とはいえ入力データの相関がありそう ==> grouping i.e. elastic net regressionにしたい。
- 決定木について
- アンサンブル学習 の目標は、単一の推定器に対する汎用性/頑健性を向上させるために、与えられた学習アルゴリズムで構築されたいくつかの基本推定器の予測を組み合わせることです。
- 平均化手法 は、いくつかの推定器を独立して作成し、それらの予測値を平均化することを原則としています。 平均して、結合された推定器は、その分散が減少するので、通常、単一の推定器よりも優れている。
- 対照的に、 ブースティング法 では、ベース推定器が順次構築され、結合推定器のバイアスを低減しようとする。 モチベーションはいくつかの弱いモデルを組み合わせて強力なアンサンブルを作り出すことです。
- https://qiita.com/nazoking@github/items/51a46256ecda598b60dd
- ExtraTreesRegressor
- 弱学習器の組み合わせとしては、一番優秀かも?https://dd1.work/nisa/03_non_lr/
- メモ
- 引用文献。RidgeやLasso。
- http://tekenuko.hatenablog.com/entry/2017/11/18/214317

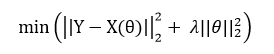
 wikipediaより
wikipediaより